Main Data Structures

 

These are the Main Data Structures

1. Arrays
2. Stacks
3. Queues
4. Linked Lists
5. Trees
6. Graphs
7. Hash Tables

1. Array

 

An array is the simplest and most widely used data structure. Other data structures like stacks and queues are derived from arrays.

Here’s an image of a simple array of size 4, containing elements (1, 2, 3 and 4).

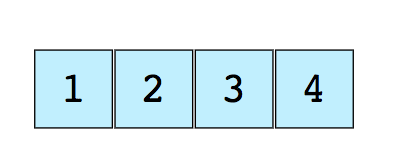
Each data element is assigned a positive numerical value called the Index, which corresponds to the position of that item in the array. The majority of languages define the starting index of the array as 0.

The following are the two types of arrays:

• One-dimensional arrays (as shown above)
• Multi-dimensional arrays (arrays within arrays)

 

Basic Operations

Following are the basic operations supported by an array.

• Traverse − print all the array elements one by one.

• Insertion − Adds an element at the given index.

• Deletion − Deletes an element at the given index.

• Search − Searches an element using the given index or by the value.

• Update − Updates an element at the given index.

   

  2. Stacks
  

 tack is a linear data structure which follows a particular order in which the operations are performed. The order may be LIFO(Last In First Out) or FILO(First In Last Out).

Mainly the following three basic operations are performed in the stack:

• Push: Adds an item in the stack. If the stack is full, then it is said to be an Overflow condition.
• Pop: Removes an item from the stack. The items are popped in the reversed order in which they are pushed. If the stack is empty, then it is said to be an Underflow condition.
• Peek or Top: Returns top element of stack.
• isEmpty: Returns true if stack is empty, else false.

3.Queue 

A Queue is a linear structure which follows a particular order in which the operations are performed. The order is First In First Out (FIFO). A good example of a queue is any queue of consumers for a resource where the consumer that came first is served first. The difference between stacks and queues is in removing. In a stack we remove the item the most recently added; in a queue, we remove the item the least recently added.

 

4. Linked List

 

A linked list is a linear data structure where each element is a separate object.
Linked list elements are not stored at contiguous location; the elements are linked using pointers.

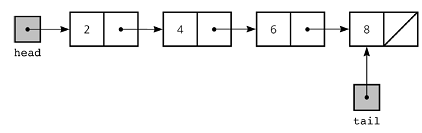
Each node of a list is made up of two items - the data and a reference to the next node. The last node has a reference to null. The entry point into a linked list is called the head of the list. It should be noted that head is not a separate node, but the reference to the first node. If the list is empty then the head is a null reference.

 

 5.Trees

 

A tree is a hierarchical data structure consisting of vertices (nodes) and edges that connect them. Trees are similar to graphs, but the key point that differentiates a tree from the graph is that a cycle cannot exist in a tree.

Trees are extensively used in Artificial Intelligence and complex algorithms to provide an efficient storage mechanism for problem-solving.

Here’s an image of a simple tree, and basic terminologies used in tree data structure:

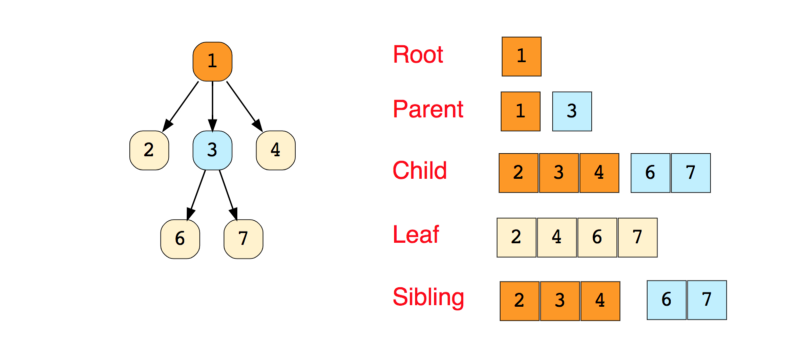
The following are the types of trees:

• N-ary Tree
• Balanced Tree
• Binary Tree
• Binary Search Tree
• AVL Tree
• Red Black Tree
• 2–3 Tree
  

 6. Graph

 

Graphs are mathematical structures that represent pairwise relationships between objects. A graph is a flow structure that represents the relationship between various objects. It can be visualized by using the following two basic components:

• Nodes: These are the most important components in any graph. Nodes are entities whose relationships are expressed using edges. If a graph comprises 2 nodes

and

• and an undirected edge between them, then it expresses a bi-directional relationship between the nodes and edge.

• Edges: Edges are the components that are used to represent the relationships between various nodes in a graph. An edge between two nodes expresses a one-way or two-way relationship between the nodes.

Types of nodes

• Root node: The root node is the ancestor of all other nodes in a graph. It does not have any ancestor. Each graph consists of exactly one root node. Generally, you must start traversing a graph from the root node.

• Leaf nodes: In a graph, leaf nodes represent the nodes that do not have any successors. These nodes only have ancestor nodes. They can have any number of incoming edges but they will not have any outgoing edges.

Types of graphs

• Undirected: An undirected graph is a graph in which all the edges are bi-directional i.e. the edges do not point in any specific direction.

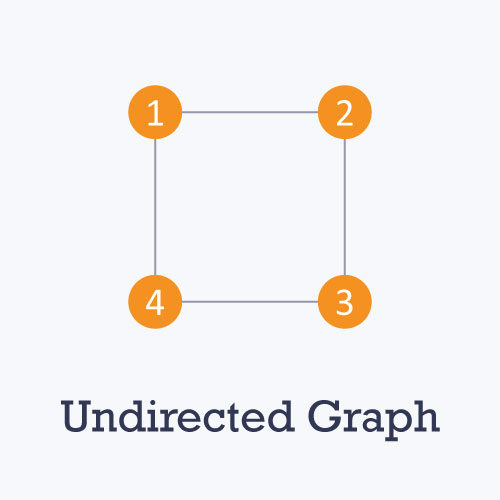
• Directed: A directed graph is a graph in which all the edges are uni-directional i.e. the edges point in a single direction.

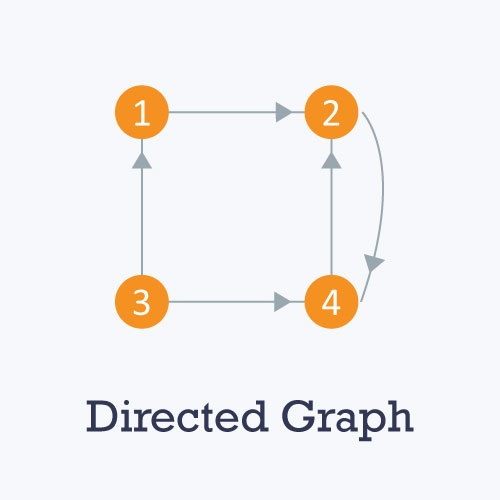
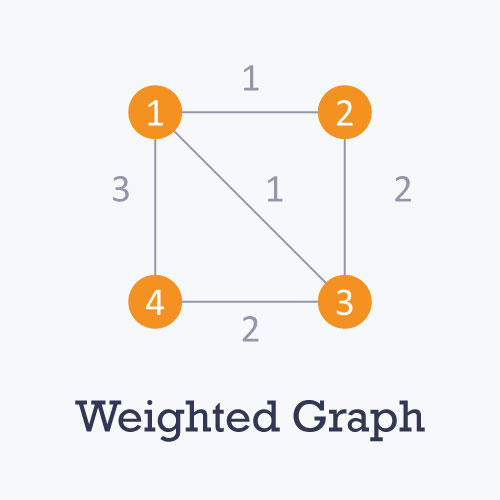
• Weighted: In a weighted graph, each edge is assigned a weight or cost. Consider a graph of 4 nodes as in the diagram below. As you can see each edge has a weight/cost assigned to it. If you want to go from vertex 1 to vertex 3, you can take one of the following 3 paths:

  • 1 -> 2 -> 3
  • 1 -> 3
  • 1 -> 4 -> 3

  Therefore the total cost of each path will be as follows: - The total cost of 1 -> 2 -> 3 will be (1 + 2) i.e. 3 units - The total cost of 1 -> 3 will be 1 unit - The total cost of 1 -> 4 -> 3 will be (3 + 2) i.e. 5 units

• Cyclic: A graph is cyclic if the graph comprises a path that starts from a vertex and ends at the same vertex. That path is called a cycle. An acyclic graph is a graph that has no cycle.

 

7. Hash Tables

 

Hash Table

Hash table is one of the most important data structures that uses a special function known as a hash function that maps a given value with a key to access the elements faster.

A Hash table is a data structure that stores some information, and the information has basically two main components, i.e., key and value. The hash table can be implemented with the help of an associative array. The efficiency of mapping depends upon the efficiency of the hash function used for mapping.

For example, suppose the key value is John and the value is the phone number, so when we pass the key value in the hash function shown as below:

Hash(key)= index;

When we pass the key in the hash function, then it gives the index.

Hash(john) = 3;

The above example adds the john at the index 3.